Grundlegende Kontostrukturen für Darlehen
-Aktiva
-Umlaufvermögen
-Sparkonto
-Anlagevermögen
-Wertgegenstand
-Fremdkapital
-Darlehen
-Hypothekendarlehen
-Aufwendungen
-Zinsen
-Hypothekenzinsen
-Hypothekengebühren
Darlehen
Dieses Kapitel erklärt, wie sie Darlehen mit GnuCash verwalten.
Grundlagen
Ein Darlehen ist eine finanzielle Transaktion, bei der jemand für die Nutzung fremden Geldes bezahlt. Es gibt viele bekannte Beispiele für Darlehen: Kreditkarte, Auto-Darlehen, Hypotheken-Darlehen oder Geschäfts-Darlehen.
Begriffsbestimmung
Es ist hilfreich, eine Begriffsbestimmung vorzunehmen, bevor im Detail erläutert wird, wie Darlehen in GnuCash im Einzelnen verwaltet werden. Die unten aufgeführten Begriffe stehen für einige der grundlegenden Ideen betreffend Darlehen. Es ist eine gute Idee, sich mit diesem Vokabular vertraut zu machen oder zumindest auf diese Liste zurückzugreifen, wenn sie in einem späteren Abschnitt einen unbekannten Fachausdruck finden.
-
Kredittilgung - der Rückzahlungsplan, der sicherstellen soll, dass das Darlehen irgendwann zurückgezahlt wird. Der Rückzahlungsplan sieht normalerweise monatliche Zahlungen vor, die in Zinszahlung und Tilgung aufgeteilt sind, wobei sich die Tilgung im Verlauf des Rückzahlungszeitraums erhöht (und die Zinszahlungen vermindert).
-
Darlehensnehmer - die Person oder Firma, die die Darlehenssumme bekommt.
-
Zahlungsausfall (Voreinstellung) - tritt auf, wenn der Darlehensnehmer unfähig ist, das Darlehen gemäß den mit dem Darlehensgeber vereinbarten Konditionen zurückzuzahlen.
-
Stundung (Zurückstellung) - ist eine zeitliche Verzögerung bei der Rückzahlung eines Darlehens
-
Säumniszuschlag - ist die vereinbarte Bedingung, für verspätete Rückzahlung.
-
Auszahlung - ist der Betrag, der an den Darlehensnehmer ausgezahlt wird. Bei einigen Darlehen erfolgt die Auszahlung in mehreren Portionen, das bedeutet, dass der Darlehensnehmer die Darlehenssumme nicht in einer Zahlung erhält.
-
Zinsen - die Kosten, die der Darlehensgeber vom Darlehensnehmer für die Nutzung des geliehenen Geldes verlangt. Diese werden normalerweise als jährlicher Prozentbetrag des Darlehensbetrages ausgedrückt, auch bekannt als Jahreszins.
-
Darlehensgeber – Die Firma oder Privatpersonen, die das Geld verleiht.
-
Darlehensgebühr - eine Bearbeitungsgebühr, die normalerweise bei Abschluss eines Darlehensvertrags von der Darlehenssumme einbehalten wird.
-
Darlehensbetrag – Der ursprüngliche Darlehensbetrag oder der Anteil des Darlehens, der noch geschuldet wird. Wenn Sie monatliche Raten für das Darlehen bezahlen, ist ein Teil davon für die Zahlung des Zinses, und ein Teil ist Rückzahlung des Darlehensbetrags.
-
Schuldschein (Eigener Wechsel) - die rechtliche, das Darlehen betreffende Vereinbarung zwischen dem Darlehensgeber und dem Darlehensnehmer.
Einrichtung der Konten
Wenn ein Darlehensnehmer sich ein Darlehen beschafft, dann normalerweise in der Absicht einen Wertgegenstand zu erwerben. Tatsächlich bedingen die meisten Darlehen den Kauf eines vorher bestimmten Anlagegegenstands, wie zum Beispiel eines Hauses. Dieser Anlagegegenstand dient als Sicherheit gegen einen Zahlungsausfall. Es gibt natürlich auch Beispiele für Darlehen, die nicht einen Wertgegenstand als Sicherheit haben, wie zum Beispiel ein Ausbildungsdarlehen.
Für die hier dargestellte Kontostruktur nehmen wir an, dass das Darlehen zum Kauf eines Wertgegenstandes verwandt wird.
Ein Darlehen ist Fremdkapital, die anfallenden Zinsen für das Darlehen sind fortlaufender Aufwand, und alle Verwaltungsgebühren, die gezahlt werden müssen, sind sonstiger Aufwand. Der Gegenstand, der mit dem Geld des Darlehens gekauft wird, ist ein Aktiva. Mit diesen Parametern können wir jetzt die grundlegende Kontohierarchie für Darlehen aufzeigen.
GnuCash besitzt eine Anzahl vordefinierter Kontostrukturen für Darlehen, wie zum Beispiel Autodarlehen und sonstige Darlehen. Um diese vorgefertigten Kontostrukturen zu nutzen, klicken Sie auf Kontenhierarchie hinzufügen und wählen Sie einen passenden Darlehenstyp.
Berechnungen
Bestimmung des Rückzahlungsplans, der periodische Zahlungen, der gesamten Rückzahlungssumme, oder der Zinsraten kann etwas kompliziert sein. GnuCash hat einen eingebauten Darlehensrechner, um diese Art von Berechnungen zu vereinfachen. Um diesen Rechner aufzurufen, gehen sie auf menu:Werkzeuge[Darlehensrechner].

Der Darlehensrechner kann dazu benutzt werden, aus jeweils vier bekannten Darlehensparametern jeden der Parameter zu berechnen: Zahlungsintervalle, Zinssatz, Aktueller Wert, Periodische Zahlungen, oder Zukünftiger Wert . Sie müssen auch die Zins- und die Zahlungsmodalitäten angeben.
-
Zahlungsintervalle – Die Anzahl der Zahlungsintervalle.
-
Zinssatz – Der Nominalzinssatz des Darlehens, bzw. der Jahreszinssatz.
-
Aktueller Wert- Der aktuelle Wert des Darlehens, beziehungsweise der augenblicklich geschuldete Geldbetrag des Darlehens.
-
Periodische Zahlung – Der pro Intervall zu zahlende Geldbetrag.
-
Zukünftiger Wert – Die zukünftige Darlehenssumme, beziehungsweise die Darlehenssumme die nach Ablauf aller Zahlungsintervalle noch geschuldet wird.
-
Zinstyp – Es gibt zwei Methoden der Verzinsung, Schrittweise und kontinuierlich. Für eine schrittweise Verzinsung wählen Sie bitte die Häufigkeit von jährlich bis täglich.
-
Zahlungen – Hier können Sie auswählen, ob die Zahlungen am Anfang oder am Ende des Zahlungsintervalls erfolgen. Weiterhin können hier die Zahlungsintervalle im Bereich von jährlich bis täglich eingestellt werden. Sowohl Zahlungen am Beginn des Intervalls als auch Vorwegzahlungen und noch geschuldetes Geld werden bei der Zinsberechnung berücksichtigt.
Beispiel: monatliche Zahlungen
Wie hoch sind die monatlichen Raten für ein dreißigjähriges Darlehen von 100.000,- € bei einem festen Zinssatz von 4 % und monatlicher Verzinsung?
Dieses Szenario wird im obigen Beispielbild dargestellt. Um die Berechnungen durchzuführen, tragen sie unter Zahlungsintervalle 360 ein (12 Monate mal 30 Jahre), Zinssatz auf 4, Aktueller Wert auf 100.000, lassen sie Periodische Zahlung frei, und setzen sie Zukünftiger Wert auf 0 (am Ende des Darlehens wollen sie schuldenfrei sein). Die Verzinsung ist monatlich, die Zahlungen werden monatlich geleistet, unter der Annahme einer Zahlung am Ende des Intervalls und schrittweiser Verzinsung. Drücken Sie jetzt den Berechnen Knopf unter den Darlehensparametern. Als Ergebnis sehen Sie -477,42 € im Feld periodische Zahlungen.
Antwort: die monatlichen Raten betragen -477,42 €
Beispiel: Zahlungsdauer
Wie lange dauert die Rückzahlung eines 22.000,- € Darlehen bei 10 % Zinssatz, monatlicher Verzinsung und einer Rückzahlung von 500,- € im Monat?
Zur Durchführung dieser Berechnungen lassen Sie Zahlungsintervalle frei, setzen den Zinssatz auf 10, Aktueller Wert auf20.000, Periodische Zahlung ist -500, und Zukünftiger Wert ist 0 (am Ende des Darlehens wollen sie schuldenfrei sein). Verzinsung ist monatlich, Zahlungen sind monatlich, unter der Annahme einer Zahlung am Ende des Intervalls und schrittweiser Verzinsung. Drücken Sie jetzt den Berechnen Knopf unter den Darlehensparametern. Als Ergebnis sehen sie 49 im Feld Zahlungsintervalle.
Antwort: Die Rückzahlung des Darlehens dauert vier Jahre und einen Monat (49 Monate).
Erweitert: Einzelheiten der Berechnung
Für die Besprechungen der mathematischen Formeln, die durch den Darlehensrechner benutzt werden definieren wir erst die folgenden Variablen.
n == Anzahl der Zahlungsperioden %i == nominaler Zinssatz PV == aktueller Wert PMT == periodische Zahlungen FV == zukünftiger Wert CF == Zinsperiode pro Jahr PF == Zahlungsperiode pro Jahr Normale Werte für CF und PF sind: 1 == jährlich 2 == halbjährlich 3 == dreimal im Jahr 4 == vierteljährlich 6 == alle zwei Monate 12 == monatlich 24 == halb monatlich 26 == alle zwei Wochen 52 == wöchentlich 360 == täglich (12 x 30 Tage) 365 == täglich
Umrechnung zwischen nominalem und effektivem Zinssatz
Wenn eine Lösung für n, PV, PNT oder FV benötigt wird, muss zuerst der nominale Zinssatz (i) in den effektiven Zinssatz (ieff) für die Zahlungsperiode umgerechnet werden. Dieser effektive Zinssatz wird dann benutzt, um die gewünschte Variable zu berechnen. Wenn eine Lösung für i benötigt wird, ergibt die Berechnung den effektiven Zinssatz (ieff). Deshalb benötigen wir Funktionen, die den nominalen Zinssatz in den effektiven Zinssatz, und den effektiven Zinssatz in den Nominalzinssatz umrechnen.
Zur Umrechnung von i nach ieff werden folgende Formeln genutzt: schrittweise Verzinsung: __ieff = (1 + i/CF)^(CF/PF) - 1__ kontinuierliche Verzinsung: __ieff = e^(i/PF) - 1 = exp(i/PF) - 1__ Zur Umrechnung von ieff nach i werden folgende Formeln genutzt: schrittweise Verzinsung: __i = CF*[(1+ieff)^(PF/CF) - 1]__ kontinuierliche Verzinsung: __i = ln[(1+ieff)^PF]__
|
Note
|
Hinweis: in den unten stehenden Gleichungen für Geldgeschäfte sind alle Zinssätze die effektiven Zinssätze, "ieff". Aus Gründen der Kürze wird statt "ieff" nur "i"benutzt. |
Die grundlegenden Finanzgleichungen
Eine Gleichung verbindet alle fünf genannten Variablen. Diese ist bekannt als die grundlegende Finanzgleichung:
__PV*(1 + i)^n + PMT*(1 + iX)*[(1+i)^n - 1]/i + FV = 0__
Dabei ist: X = 0 für Zahlungen am Ende des Zeitraums und
X = 1 für Zahlungen am Anfang des Zeitraums.
Aus dieser Gleichung können Funktionen abgeleitet werden, um einzelne Variablen zu berechnen. Für eine ausführliche Beschreibung der Ableitung dieser Gleichungen lesen Sie bitte die Kommentare in der Datei src/calculation/fin.c im GnuCash Quelltext. Die Variablen A, B, und C werden zuerst definiert, um die nachfolgenden Gleichungen übersichtlicher zu machen.
__A = (1 + i)^n - 1__ __B = (1 + iX)/i__ __C = PMT*B__ __n = ln[(C - FV)/(C + PV)]/ln((1 + i)__ __PV = -[FV + A*C]/(A + 1)__ __PMT = -[FV + PV*(A + 1)]/[A*B]__ __FV = -[PV + A*(PV + C)]__ Die Auflösung nach dem Zinssatz wird in zwei Fälle unterteilt. Der einfache Fall mit PMT == 0 ergibt die Gleichung: __i = [FV/PV]^(1/n) - 1__
Der Fall, wo PMT != 0 ist ziemlich komplex und wird hier nicht behandelt. Statt eine exakt lösbare Funktionen zur Bestimmung des Zinssatzes für den Fall PMT !=0 zu benutzen, wird ein interaktiver Prozess verwendet. Bitte lesen Sie die Datei src/calculation/fin.c für eine ausführliche Erklärung.
Beispiel: monatliche Zahlungen
Jetzt wollen wir das Beispiel Beispiel: monatliche Zahlungen, erneut berechnen, diesmal aber statt mit dem Darlehensrechner mit den vorgestellt mathematischen Formeln. Wie hoch sind die monatlichen Raten für ein dreißigjähriges Darlehen von 100.000 € bei einem festen Zinssatz von 4 % und monatlicher Verzinsung?
Zuerst wollen wir die Variablen bestimmen: n = (30*12) = 360, PV = 100000, PMT = unbekannt, FV = 0, i = 4%=4/100=0.04, CF = PF = 12, X = 0 (am Ende der Zahlungsintervalle).
Der zweite Schritt ist die Umwandlung des nominalen Zinssatzes (i) in den effektiven Zinssatz (ieff). Da der Zinssatz monatlich berechnet wird, haben wir schrittweise Verzinsung, und wir benutzen die Formel: ieff = (1 + i/CF)^(CF/PF) - 1, durch einsetzen der Werte ergibt sich ieff = (1 + 0.04/12)^(12/12) - 1, oder ieff = 1/300 = 0.0033333.
Jetzt können wir A und B berechnen. A = (1 + i)^n - 1 = (1 + 1/300)^360 - 1 = 2.313498. B = (1 + iX)/i = (1 + (1/300)*0)/(1/300) = 300.
Mit A und B können wir die PMT berechnen. PMT = -[FV + PV*(A
1)]/[A*B] = -[0 + 100000*(2.313498 + 1)] / [2.313498 * 300] =
-331349.8 / 694.0494 = -477.415296 = -477.42.
Antwort: die monatlichen Raten betragen 477,42 €.
Hypothekendarlehen (wie wird es gemacht)
Ein Hypothekendarlehen kann verwaltet werden mit der Kontenhierarchie in Einrichtung der Konten.
Als Beispiel nehmen wir an, Sie haben 60.000 € auf ihrem Bankkonto, und Sie kaufen ein Haus für 150.000,- €. Das Darlehen kostet 6 % jährliche Zinsen und hat Verwaltungskosten (Abschlussgebühren usw.) von 3 %. Sie beschließen, davon 50.000,- € als Anzahlung zu leisten und müssen deshalb 103.000,- € ausleihen. das ergibt für sie 100.000,- €, nachdem die Abschlussgebühren bezahlt sind (3 % von 100.000 €).
Die Kontostände vor dem Darlehen:

Der Kauf des Hauses wird mit einer Splitbuchung im Konto Aktiva:Anlagevermögen:Haus gebucht, 50.000,- € kommen dabei von ihrem Bankkonto (Ihre Anzahlung), und 100.000,- € kommen von dem Darlehen. Sie können die Abschlussgebühren in der selben Splitbuchung buchen, dann erhöht sich das Hypothekendarlehen auf 103.000,- € inklusive Abschlussgebühren.
Konto |
Einzahlung |
Auszahlung |
Aktiva:Anlagevermögen:Haus |
150.000,- € |
|
Aktiva:Umlaufvermögen:Sparkonto |
50.000,- € |
|
Fremdkapital:Darlehen:Hypothekendarlehen |
103.000,- € |
|
Aufwand:Hypothekengebühren |
3.000,- € |
Die Teilbuchung sieht in Akitva:Sachanlagen:Haus Account:

Das ergibt folgende Kontostände:
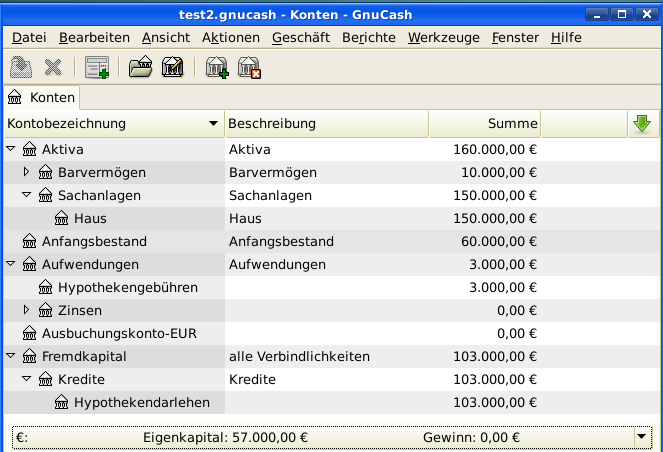
Ein persönliches Darlehen an einen Freund (wie wird es gemacht)
Nicht immer leihen Sie sich Geld von der Bank, manchmal leihen sie sich Geld von Ihren Familienangehörigen, oder vielleicht verleihen Sie Geld an einen Freund. Dieses Kapitel wird einen Weg beschreiben, Ihr persönliches Darlehen an einen Freund zu behandeln.
Dieses Beispiel basiert auf den folgenden allgemeinen Kontostrukturen.
-Aktiva
-Bank
-Bankkonto
-ihnen geschuldetes Geld
-Person
-Ertrag
-Zinsertrag
-Person
Dieses Beispiel zeigt, wie Sie die Entwicklung eines persönlichen Darlehens von 2.000,- € an ihren Freund Peter verfolgen
Darlehensparameter
Peter möchte 2.000,- € von Ihnen ausleihen und diesen Betrag während der nächsten 18 Monate zurückzahlen. Weil er Ihr Freund ist, einigen Sie sich auf einen jährlichen Zinssatz von 5 %.
Zusammenfassend haben wir also folgende Details für Peters Darlehen:
-
Darlehenssumme - 2.000,- €
-
Darlehenskonditionen - 18 Monate mit 12 Zahlungen per Jahr
-
jährlicher Zinssatz: 5 %
-
monatliche Zahlungen: ??
Also wie berechnen Sie die monatlichen Raten?
Für die Berechnungen haben Sie verschiedene Möglichkeiten, zum Beispiel Papier und Bleistiften, Linux Rechner, OpenOffice Calc-Modul, aber aber an einfachsten ist die Benutzung des GnuCashDarlehensrechner. Dieser errechnet Ihnen, dass die monatliche Zahlung 115,56 € betragen sollte.
Aber um eine ordentliche Buchführung zu machen, müssen Sie wissen, welcher Anteil dieser Summe Zinsen sind und welcher Anteil Tilgung des Darlehens. Dafür brauchen Sie ein leistungsfähiges Werkzeug, etwa wie das Calc Modul in OpenOffice und im besonderen die PMT Funktion.

Konten für das Darlehen
Wir beginnen mit folgender Kontenhierarchie (alle Konten haben dieselbe Währung, in diesem Fall Euro)
Aktiva:Bank:EUR Aktiva:Ihnen geschuldetes Geld:Peter Ertrag: Zinsertrag:Peter Vermögen:Anfangskontostand:EUR
Geld verleihen
Wenn Sie das Geld an ihren Freund verliehen haben, haben Sie tatsächlich Geld von einem Aktiva (Girokonto Sparbuch oder ähnlichem) zu einem anderen Aktiva Ihnen geschuldetes Geld verschoben. Um dies zu buchen, fügen Sie folgende Buchung im Konto Aktiva:Ihnen geschuldetes Geld:Peter ein.
Konto |
Einzahlung |
Auszahlung |
Aktiva:Ihnen geschuldetes Geld:Peter |
2.000,- € |
|
Aktiva:Bank:EUR |
2.000,- € |
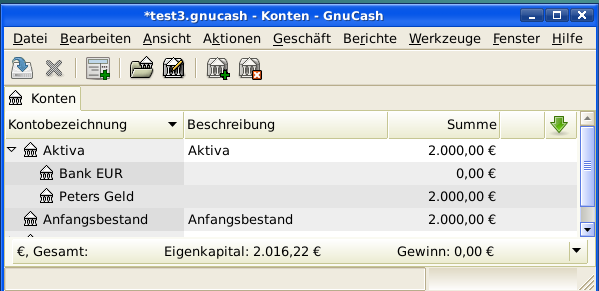
Erste Zahlung
Wenn Sie die erste Rückzahlung (115,56 €) erhalten, müssen Sie feststellen, wie viel davon Tilgung des Darlehens und wie viel Zinszahlung ist.
-
Offen stehender Darlehensbetrag für diese Periode = 2,000,- €
-
Zahlung pro Monat = 115,56 €
-
Aufteilung der Zahlung
-
5%/12 * $2,000 = 8,33 € Zinsen
-
115,56 € - 8,33 € = 107,23 € Tilgung
Dies kann durch die folgende GnuCash Buchung umgesetzt werden.
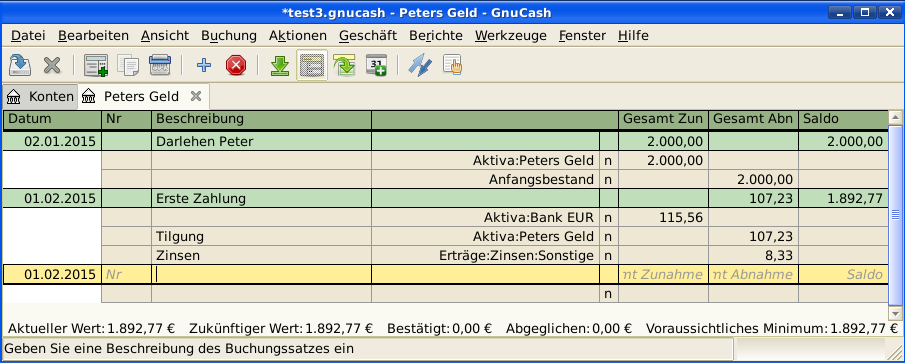
Der Kontostand in Peters Darlehen ist nun 2.000,- € - 107,23 € = 1.892,77 €
Zweite Zahlung
Wenn Sie die zweite Rückzahlung (115,56 €) erhalten, müssen Sie wieder feststellen, wie viel davon Tilgung des Darlehens und wie viel Zinszahlung ist.
-
Offen stehender Darlehensbetrag für diese Periode = 1.892,77
-
Zahlung pro Monat = 115,56
-
Aufteilung der Zahlung
-
5%/12 * 1.892,77 = 7,89 Zinsen
-
115,56 € - 7,89 € = 107,67 € Tilgung
Dies kann durch die folgende GnuCash Buchung umgesetzt werden.

Der Kontostand in Peters Darlehen ist nun 1.892,77 € - 107,67 € = 1.785,10 €
die Kontostände sehen jetzt folgendermaßen aus

Wie Sie sehen können, verändert sich der Anteil der Zinsen, und der Anteil an Tilgung. Sie müssen deshalb für jede Zahlung, die Sie empfangen, die richtigen Beträge für Ihre verschiedenen Splitbuchung berechnen.
Der Zinsanteil wird mit jeder Zahlung kleiner und kleiner (da er von einer kleineren Darlehenssumme berechnet wird), bis er bei der letzten Zahlung gegen null geht. Sehen Sie dazu auch die Zahlen in der Berechnung (Detaillierte Überblick über das Privatdarlehen an Peter).
Kfz-Darlehen (wie wird es gemacht)
Das Kfz-Darlehen wird genauso behandelt, wie das Immobiliendarlehen. Der einzige Unterschied sind andere Kontobezeichnungen und andere Zinskonditionen.
Grundlegende Kontostrukturen für Darlehen
-Aktiva
-Umlaufvermögen
-Sparkonto
-Anlagevermögen
-Kfz
-Fremdkapital
-Darlehen
-Kfz-Darlehen
-Aufwendungen
-Zinsen
-Zinsen Kfz-Darlehen
-Gebühren Kfz-Darlehen
Weitere Informationen finden Sie unter Hypothekendarlehen (wie wird es gemacht)
Abgleich eines Darlehnskontos (Wie wird es gemacht)
Der Abgleich eines Darlehnskontos unterscheidet sich nicht vom Abgleich eines Bankkontos, oder eines Kreditkartenkontos.
Während des Abgleichzeitraums sollten Sie alle das Darlehen betreffenden Zahlungen gebucht haben. Jede davon betrifft das Konto
Fremdkapital:Darlehen:__++Darlehen++__. zum Beispiel vermindert eine Rückzahlung eines Darlehens ihr __Bankkonto__, und erhöht die Konten __Darlehen__,__Darlehenszins__ und eventuell __Darlehensgebühr__.
Wenn Ihnen die aktuelle Darlehensabrechnung vorliegt, öffnen Sie das Darlehenskonto, starten den Abgleichassistenten und markieren all die Buchungen, die sie aufgezeichnet haben. Wenn Sie damit fertig sind, sollte die Differenz 0 sein und wenn nicht, dann müssen Sie die Buchungen in ihrem Konto mit dem Kontoauszug vergleichen, um die Abweichung festzustellen. Wenn Sie die Abweichung gefunden und korrigiert haben, beträgt die Differenz 0, das Konto ist abgeglichen, und sie können den Abgleichassistenten abschließen.
Weitere Informationen zum Abgleich finden Sie unter [txns-reconcile1]
Verkauf eines Hauses oder eines Kfz (Wie wird es gemacht)
Für die Buchung Ihres Hausverkaufs gibt es verschiedene Möglichkeiten in GnuCash. An dieser Stelle werden wir zwei von Ihnen behandeln. Bei einer buchen Sie nur den Einkaufs- und den Verkaufspreis. Bei der anderen haben Sie die Bewegungen auf dem Häusermarkt verfolgt, und im Laufe der Zeit diverse unrealisierte Gewinne gebucht.
Einfache Buchung
Bei dieser Methode buchen Sie lediglich die Kaufs- und Verkaufspreise.
Lassen Sie uns zwei Beispiele eines Hausverkaufs durcharbeiten, ein Verkauf mit Gewinn und einer mit Verlust. Wenn Sie stattdessen ein Kfz verkaufen wollen, ersetzen Sie einfach das Hauskonto durch das Kfz-Konto.
-Aktiva
-Anlagevermögen
-Haus
-Umlaufvermögen
-Sparkonto
-Ertrag
-langfristige Kapitalerträge
-Haus
-
Sie haben vor einiger Zeit ein Haus für 300.000,- € gekauft, und jetzt haben Sie es geschafft es für 600.000,- € zu verkaufen. Wie können Sie das buchen?
Um diesen Vorgang aufzuzeichnen müssen Sie Ihr Bankkonto um 600.000,- € erhöhen, und irgend ein anderes Konto um 600.000,- € verringern. Das Hauskonto hat nur einen Kontostand von 300.000,- €, den damaligen Kaufpreis. Sie buchen diesen Betrag auf Ihr Bankkonto, aber es fehlen immer noch 300.000,- €. Diesen Betrag holen Sie von dem Konto Ertrag:langfristige Kapitalerträge:Haus. Die Splitbuchung, die Sie in Ihr Bank-Konto (Aktiva:Umlaufvermögen:Sparkonto)buchen, sollte so aussehen.
Konto
Einzahlung
Auszahlung
Aktiva:Umlaufvermögen:Sparkonto
600.000,- €
Aktiva:Anlagevermögen:Haus
300.000,- €
Ertrag:langfristige Kapitalerträge:Haus
300.000,- €
-
Sie haben vor einiger Zeit ein Haus für 300.000,- € gekauft, aber wegen eines neugebauten Flughafens können sie es nur noch für 230.000,- € verkaufen. Wie können Sie das buchen?
Um diesen Vorgang aufzuzeichnen müssen Sie Ihr Bankkonto um 230.000,- € erhöhen, und irgend ein anderes Konto um 230.000,- € verringern. Das Hauskonto hat einen Kontostand von 300.000,- €, das ist mehr als der Preis für den Sie verkauft haben Sie buchen 230.000,- € auf ihr Bankkonto, haben danach aber immer noch 70.000,- € auf ihrem Hauskonto, die auch noch abgebucht werden müssen. Diesen Betrag buchen sie auf ihr Konto Ertrag:langfristige Kapitalerträge:Haus, was einen Verlust bedeutet. Die Splitbuchung, die Sie in Ihr Bank-Konto (Aktiva:Umlaufvermögen:Sparkonto)buchen, sollte so aussehen.
Konto
Einzahlung
Auszahlung
Aktiva:Anlagevermögen:Haus
300.000,- €
Aktiva:Umlaufvermögen:Sparkonto
230.000,- €
Ertrag:langfristige Kapitalerträge:Haus
70.000,- €
Eine komplexere Betrachtung
In diesem Beispiel werden wir uns mit etwas komplexeren Prinzipien der Buchführung beschäftigen. Weitere Einzelheiten zu diesem Thema finden Sie auch unter [chapter_capgain]
Hier werden wir uns nur mit dem Fall befassen, dass der augenblickliche Wert des Hauses gut geschätzt werden konnte. Für die anderen Fälle (Über- und Unterschätzung), lesen Sie bitte [chapter_capgain].
-Aktiva
-Anlagevermögen
-Haus
-Anschaffung
-unrealisierter Gewinn
-Umlaufvermögen
-Sparkonto
-Ertrag
-realisierter Gewinn
-Haus
-unrealisierter Gewinn
-Haus
Vor einiger Zeit haben Sie ein Haus für 300.000,- € gekauft und während er Jahre haben Sie den Häusermarkt beobachtet und einen geschätzten Zeitwert Ihres Hauses ermittelt. Der augenblickliche Marktwert zum Zeitpunkt des Verkaufs beträgt 600.000,- €.
Der Unterschied zwischen 600.000,- € (geschätzter Marktwert) und 300.000,- € (Kaufpreis) ist der augenblickliche unrealisierte Gewinn. Deshalb haben sie einen Betrag von 300.000,- € auf Ihrem Konto Aktiva:Anlagevermögen:Haus:unrealisierter Gewinn.
Wie wird dieser Verkauf eingegeben?
Um diesen Verkauf einzugeben, muss dem Bankkonto die Verkaufsumme von 600.000,- € gutgeschrieben werden und gleichzeitig andere Konten mit der Summe von 600.000,- € belastet werden. Zuerst muss der unrealisierte Gewinn auf Ihren Ertrag-Konten in einen realisierten Gewinn umgewandelt werden. Zum Schluss müssen Sie die Gesamtsumme von Ihren Aktiva:Anlagevermögen:Haus Unterkonten auf Ihr Bankkonto übertragen.
Die Buchung, die Sie in Ihrem Konto Ertrag:realisierter Gewinn:Haus eingeben, sollte folgendermaßen aussehen.
Konto |
Einzahlung |
Auszahlung |
Ertrag:realisierter Gewinn:Haus |
300.000,- € |
|
Ertrag:unrealisierter Gewinn:Haus |
300.000,- € |
Die Buchung, die Sie in Ihrem Konto Aktiva:Umlaufvermögen:Sparkonto eingeben, sollte folgendermaßen aussehen.
Konto |
Einzahlung |
Auszahlung |
Aktiva:Umlaufvermögen:Sparkonto |
600.000,- € |
|
Aktiva:Anlagevermögen:Haus:Anschaffung |
300.000,- € |
|
Aktiva:Anlagevermögen:Haus:unrealisierter Gewinn |
300.000,- € |
Nach Eingabe dieser Buchung sehen Sie, dass Ihr Hausvermögen jetzt den Wert null hat, der Betrag auf ihrem Sparkonto wurde um 600.000,- € erhöht, und zuletzt hat hat sich der Betrag unter Ertrag:realisierte Gewinn auf 300.000,- € erhöht.